BAD Day 1: Additional

1. Probability distributions

These can be either discrete or continuous (e.g. uniform, bernoulli, normal), and are defined by a density function $ p(x) $ or $f(x)$.

1.1 Bernoulli distribution Be(p)

Flip a coin $(T = 0, H = 1)$. The probability of H is 0.1

In [1]:

x <- 0:1
f <- dbinom(x, size = 1, prob = .1)

# plotting the distribution
plot(x, f, xlab = "x", ylab = "density", type = "h", lwd = 5, col = 'mediumpurple')

png

1.2 Binomial Random sampling

Generate 100 observations from Be (0.1)

In [2]:

set.seed(100)
x <- rbinom(100, size = 1, prob = .1)

# plotting
hist(x, col = 'mediumpurple')
box()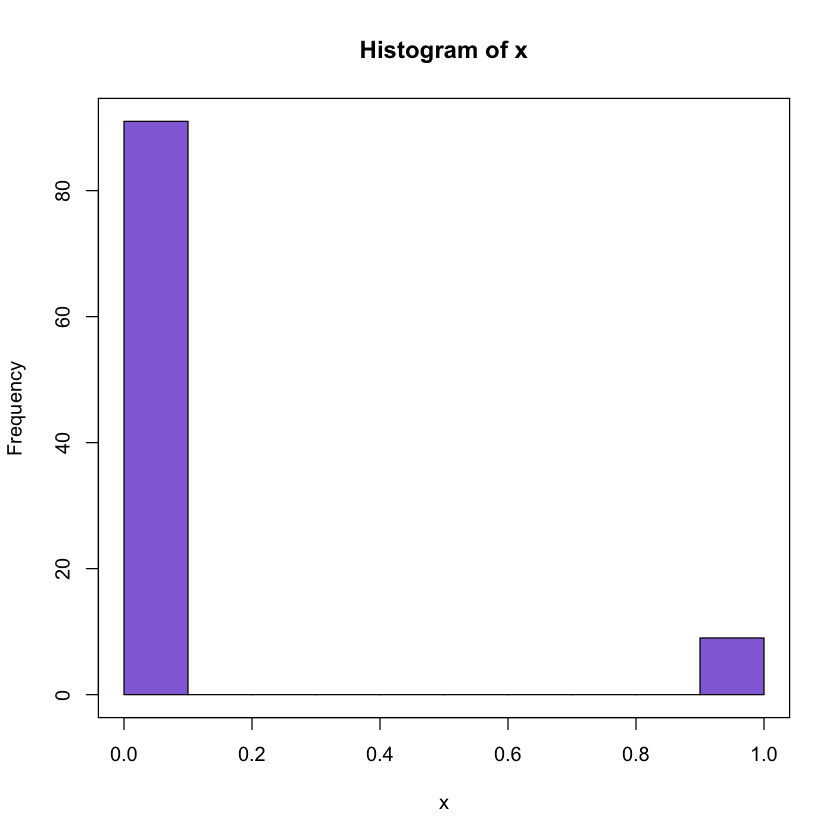

png

1. 3 Normal distribution

The data values are members of a normally distributed population with mean $\mu$ and variance $\sigma^2$.

The value of the distribution function is given by $P(X \leq x)$, the probability of the population to have values smaller than or equal to $x$.

In [3]:

x <- seq(-4,4,.1)
f <- dnorm(x, mean = 0, sd = 1)

# plotting
plot(x, f, xlab = "x", ylab = "density", lwd = 5,type = "l")
arrows(1, 0.05, 1, 0.1, lwd = 3, col = 'slateblue')
text(x = 0, y = 0.02, label = 'Note the area under the curve \n is the probability of
having an observation  between 0 and 2.')

abline(v = c(0,2), col = 'grey', lty = 5)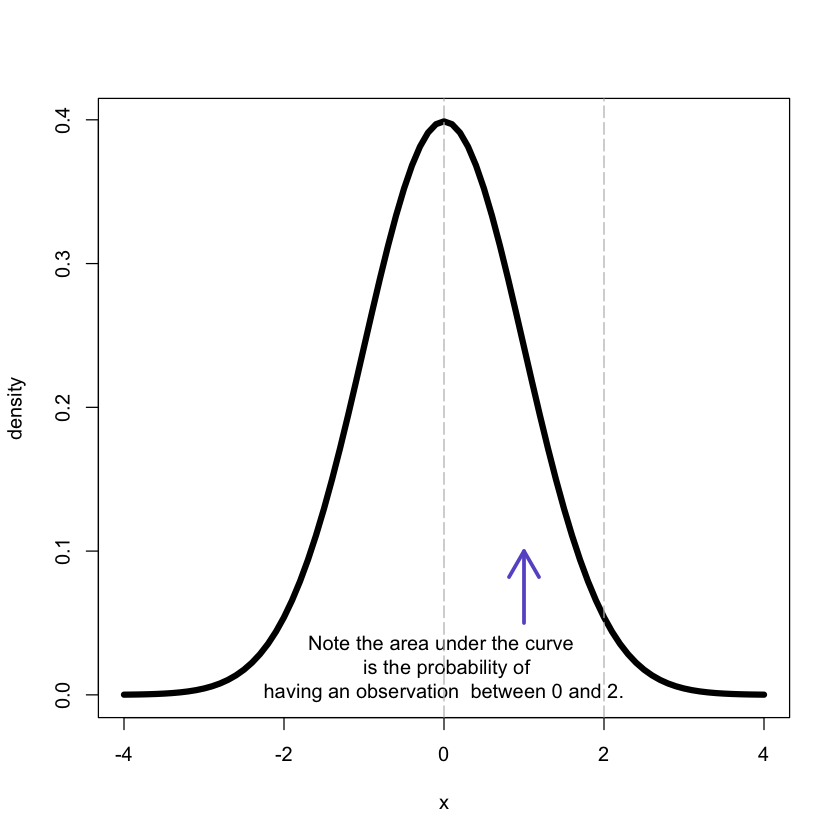

png

1.4 Normal Random sampling

Generate 1000 observations from N(0,1)

In [4]:

set.seed(100)
x <- rnorm(100, mean = 0, sd = 1)
hist(x, col = 'mediumpurple', border = 'white')
box()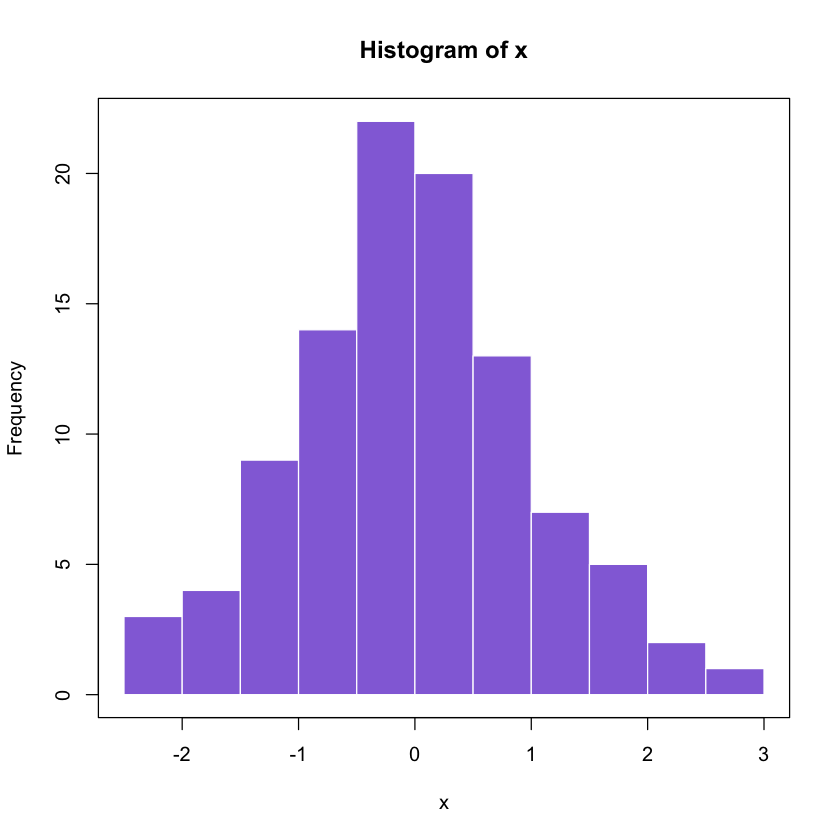

png

Histograms can be used to estimate densities!

1.5 Overview

For practical computations R has built-in functions for the binomial, normal, Chi-squared distributions, among others. Where d stands for density, p for (cumulative) probability distribution, q for quantiles, and r for drawing random samples e.g.

Distribution	parameters	density	distributon
random sampling	quantiles
Binomial	n, p	dbinom(x, n, p)	pbinom(x, n, p)
rbinom(10, n, p)	qbinom($\alpha$, n, p)
Normal	$\mu, \sigma$	dnorm(x, $\mu, \sigma$)	pnorm(x, $\mu,
\sigma$)	rnorm(10, $\mu, \sigma$)	qnorm($\alpha$,$\mu, \sigma$)
Chi-squared	m	dchisq(x, m)	pchisq(x, m)
rchisq(10,m)	qchisq($\alpha$, m)

2. Descriptive statistics

2.1 Quantiles

(Theoretical) quantiles:

The p-quantile is the value with the property that there is a probability p of getting a value less than or equal to it.

In [5]:

q90<-qnorm(.90, mean = 0, sd = 1)
x<-seq(-4,4,.1)
f<-dnorm(x, mean = 0, sd = 1)

In [6]:

# plotting
plot(x, f, xlab = "x", ylab = "density", type = "l", lwd = 4)
abline(v = q90, col = 'mediumpurple', lwd = 5)
arrows(2.5, 0.35, 1.5, 0.35, lwd = 3, col = 'midnightblue')
text(x = 2.8, y = 0.3, label ='90% of the prob \n is on the left of the
purple vertical line');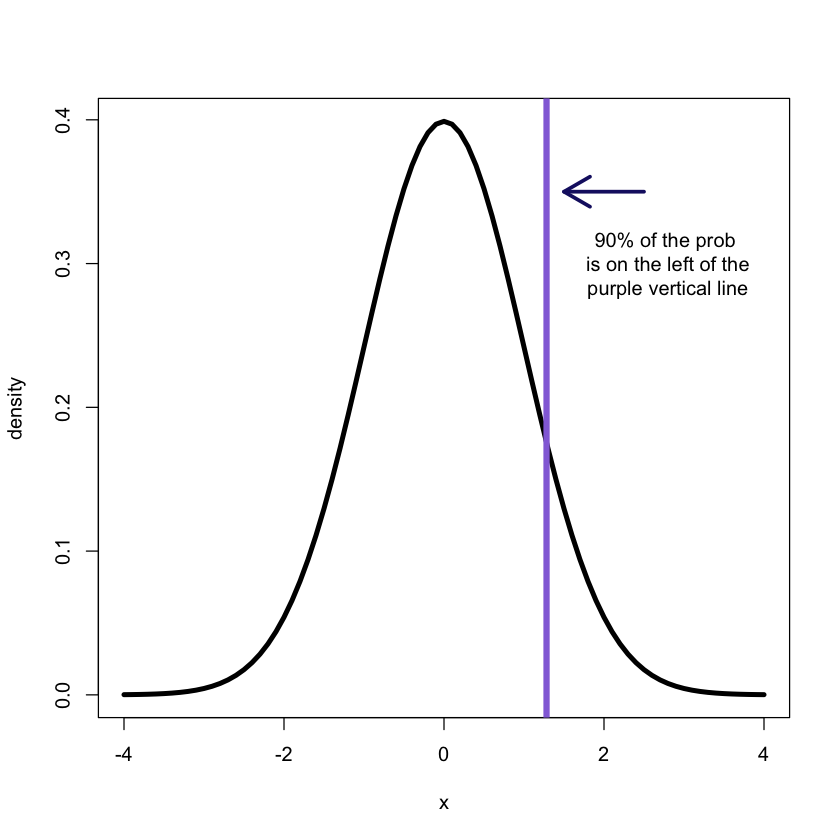

png

Empirical quantiles:

The p-quantile is the value with the property that p% of the observations are less than or equal to it.

They can be easily obtained in R:

In [7]:

x<-rnorm(100, mean = 0, sd = 1)
quantile(x)

0%: -2.13649385561006
25%: -0.431830039618815
50%: -0.072877791466942
75%: 0.446190752401337
100%: 2.16860031716614

In [8]:

quantile(x,probs = c(.1,.2,.9))

10%: -0.863526139969441
20%: -0.516638898288344
90%: 1.01977663867239

2.2 Statistical summary

We often need to quickly quantify a data set. This can be done using a set of summary statistics (e.g mean, median, variance, standard deviation).

In [9]:

set.seed(100)
x<-rnorm(100, mean = 0, sd = 1)

# Getting the mean
mean(x)

0.00291256261996373

In [10]:

# Getting the median
median(x)

-0.0594198974465339

In [11]:

# Getting the IQR
IQR(x)

1.26473767173818

In [12]:

# Getting the variance
var(x)

1.04184965729599

In [13]:

# Getting a general summary
summary(x)

     Min.   1st Qu.    Median      Mean   3rd Qu.      Max.
-2.272000 -0.608800 -0.059420  0.002913  0.655900  2.582000

You can use the summary function on almost any R object! (remmber R is an object oriented language, hence it comprises methods and classes)

2.3 Box-plots: understanding the plots

In [14]:

install.packages('shape')
library('shape')

In [15]:

set.seed(100)
x<-rnorm(100, mean = 0, sd = 1)
x = c(4.2, x)  # Adding an outlier for demonstration purposes only
boxplot(x)

# generates labels for the various components
labels <- c('Lower bound', '25% quantile', 'Median', '75% quantile',
            'Upper bound')
text(y = boxplot.stats(x)$stats, labels = labels, x = 1.35, col = 'mediumpurple')
text(y = 4.2, x = 1.35, label = 'Outlier', col = 'gray26')

# show the inter quantile range
segments(0.75, -2.27, 0.75, 0.7, col = 'midnightblue', lwd = 2)


Arrowhead(c(0.75,0.75),c(-0.58,0.7), angle = 90,
         arr.col = 'midnightblue', arr.length = 0.15, arr.width =0.25,
          arr.type = 'triangle');

Arrowhead(c(0.75, 0.75),c(-0.58, -2.27), angle = 270,
         arr.col = 'midnightblue', arr.length = 0.15, arr.width =0.25,
          arr.type = 'triangle');

text(y = c(0,-1.5), x = c(0.65, 0.65), label = c('IQR', '1.5 x IQR'),
     col = 'midnightblue')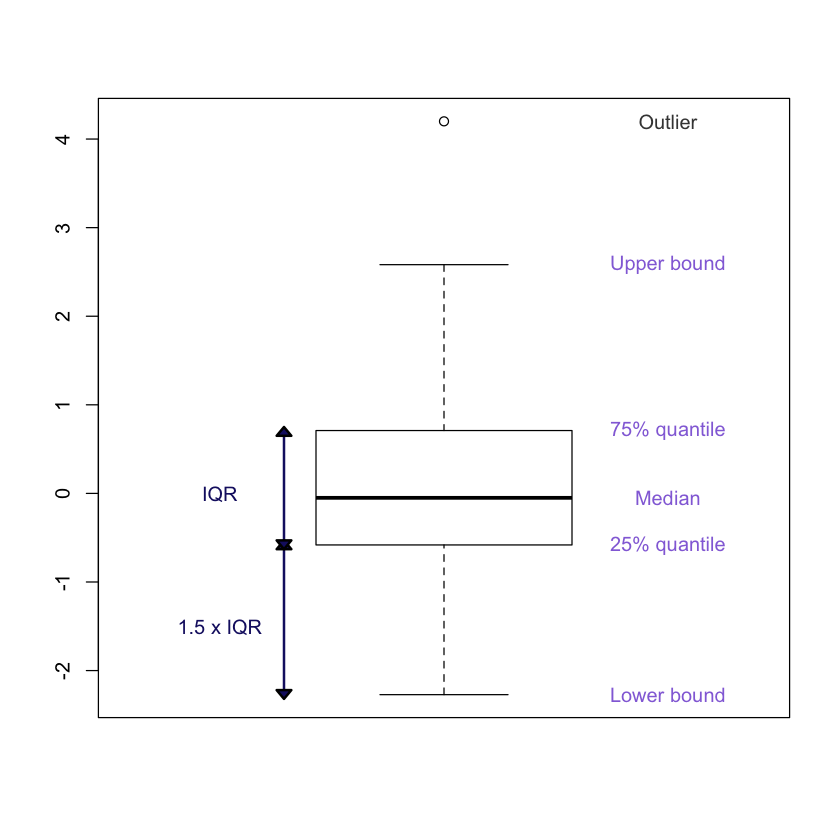

png

The median of the sampple is denoted by the horizontal line within the boxplot. The IQR corresponds to IQR = 75% quantile -25% quantile

In [16]:

IQR(x)

1.291372268193

2.4 QQ plot

Many statistical methods make some assumptions about the distribution of the data.

The quantile quantile (QQ) plot provides a mean to visually verify such assumptions.

Also, the QQ-plot shows the theoretical quantile versus the empirical quantiles. If the distribution assumed (theoreticall) is indeed correct, the result will be a straight line.

In [17]:

set.seed(100)
x<-rnorm(100, mean = 0, sd = 1)
qqnorm(x)
qqline(x, col = 'mediumpurple', lwd = 3)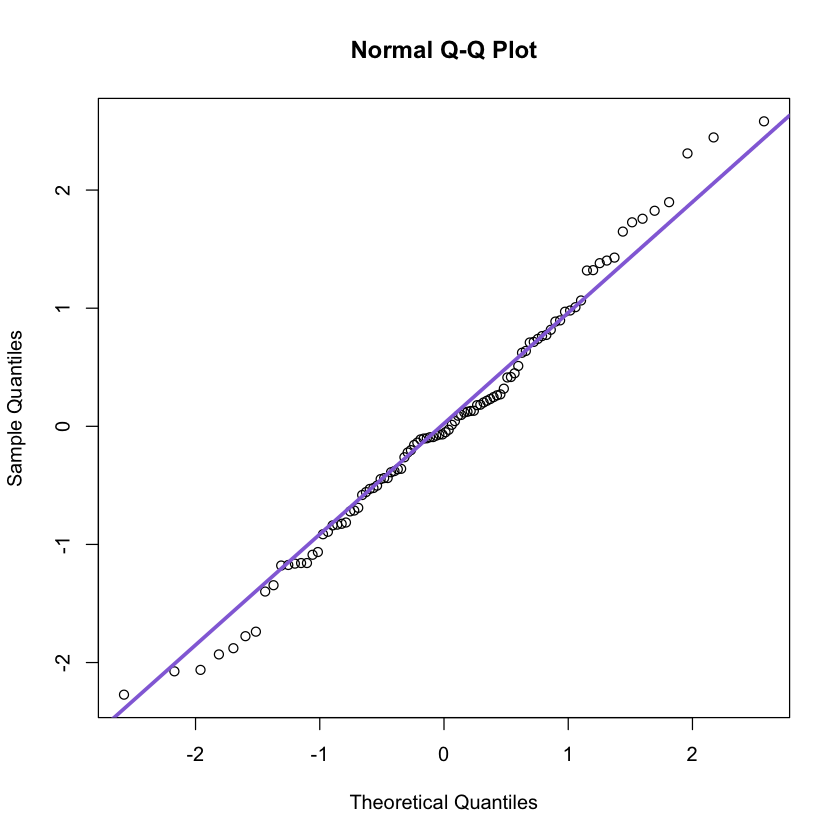

png

Note this is valid only for normal distributions!

In [18]:

set.seed(100)
x<-rt(100, df = 2)

qqnorm(x)
qqline(x, col = 'mediumpurple', lwd = 3)

png

Clearly the `t` distribution with two degres of freedom is different from

the normal distribution.

In [19]:

x<-seq(-4,4,.1)
f1<-dnorm(x, mean = 0, sd = 1)
f2<-dt(x, df = 2)

plot(x, f1, xlab = "x", ylab = "density",lwd = 3,type = "l")
lines(x, f2, xlab ="x",ylab = "density",lwd = 3,col = 'mediumpurple')
legend('topright', legend = c('Normal', 'l2'), col = c('black', 'mediumpurple'),
      lwd = 3)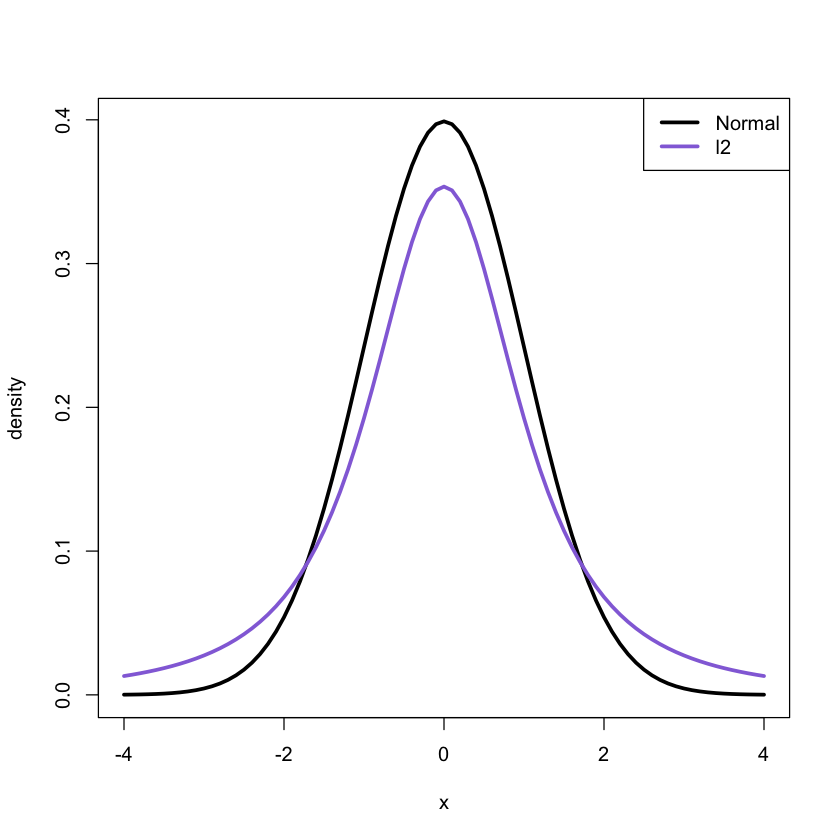

png

Comparing two samples

In [20]:

set.seed(100)
x<-rnorm(100, mean = 0, sd = 1)
y<-rnorm(100, mean = 0, sd = 1)
qqplot(x,y)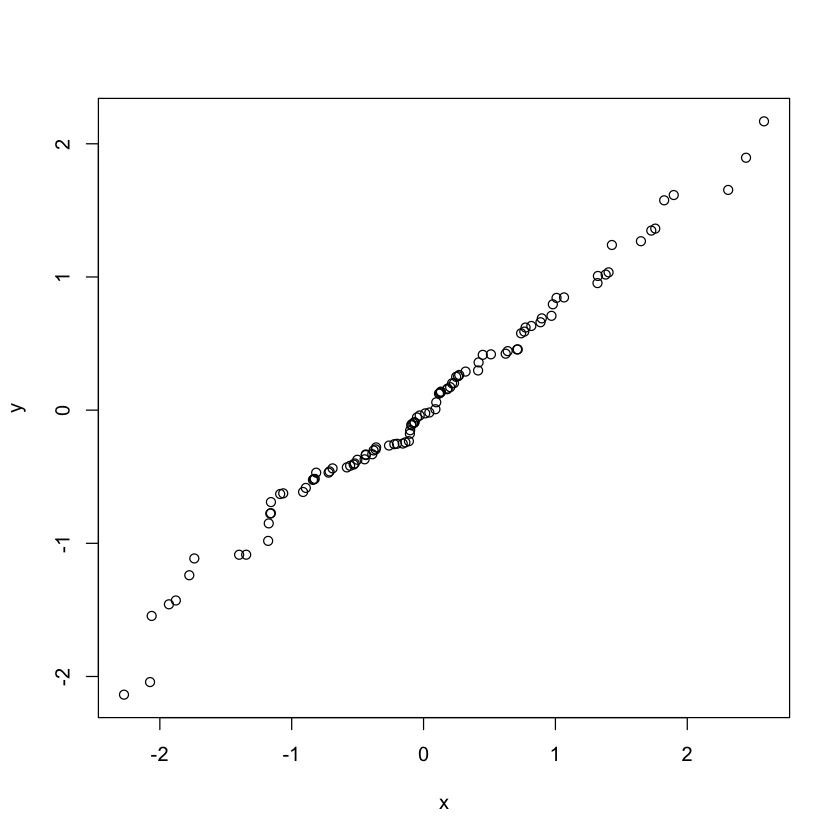

png

In [21]:

set.seed(100)
x<-rt(100, df = 2)
y<-rnorm(100, mean = 0, sd = 1)
qqplot(x,y)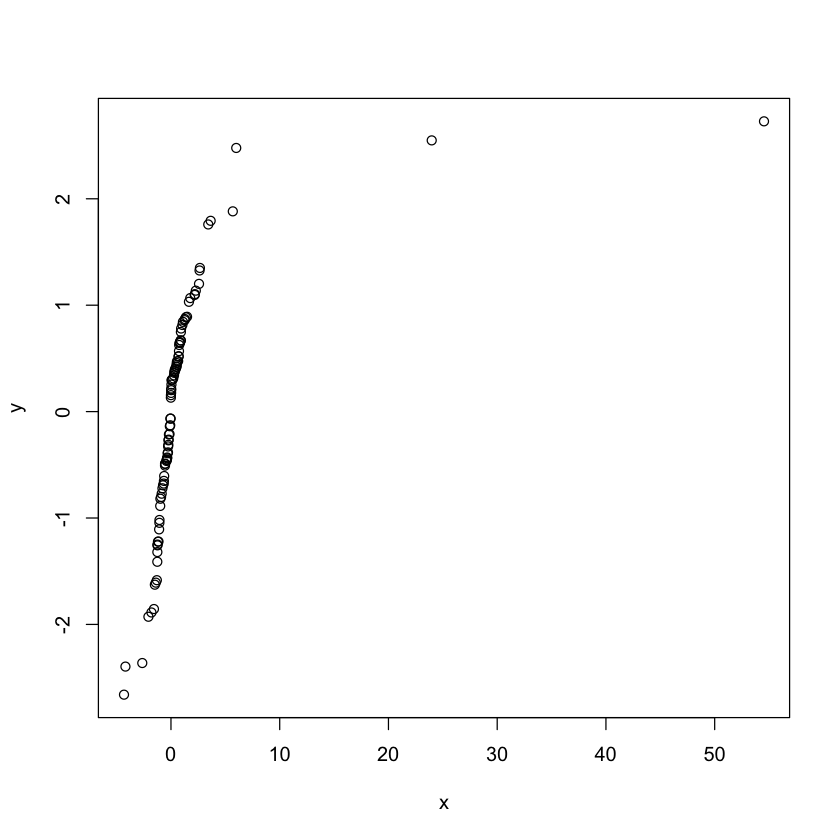

png

Exercise: Try with different values of df

2.5 Scatter plots

Biological data sets often contain serveal variables. Hence these data sets are multivariate. Scatter plots allow us to look at two variables at a time.

In [22]:

### need to add the plot
### code missing

What can you tell about this data?

This kind of plots can be used to asses independence

2.6 Scatter plots vs. correlation

Note that in the previous example the correlation between the two variables was 0.23

Note that correlation is only good for linear dependence.

In [23]:

set.seed(100)
theta<-runif(1000, 0, 2*pi)
x<-cos(theta)
y<-sin(theta)
cor(x, y)
plot(x,y)

-0.0532811841413791

png

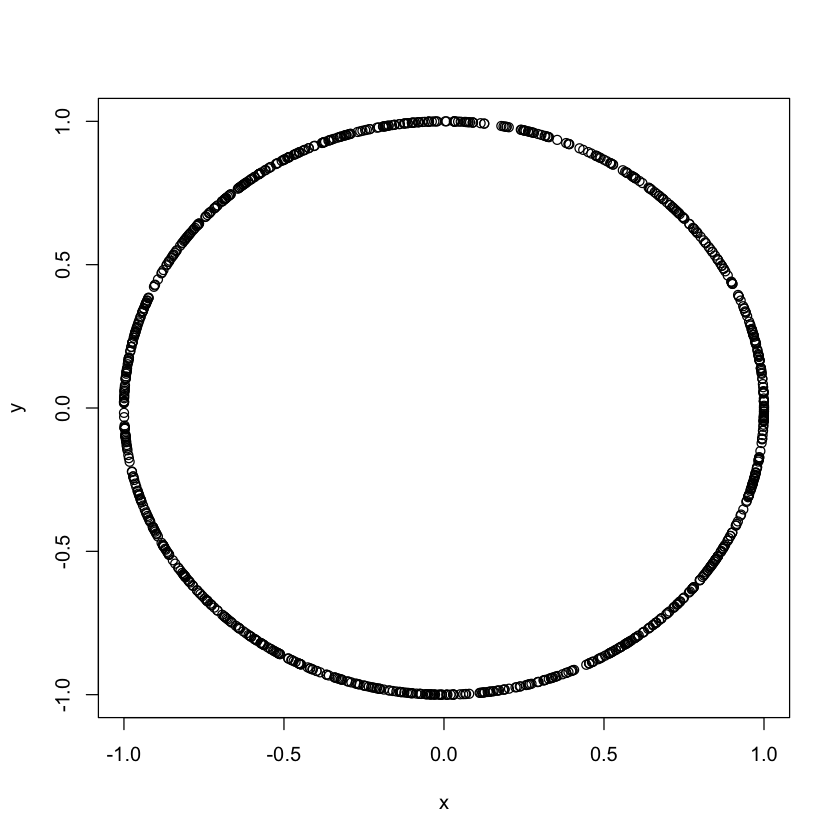
What is the correlation?